Deep neural networks came around, where what you throw onto the problem is loads of imaging data with which you train these highly overparameterized models, and all of a sudden they outperform everything else that we have done before.
Mathematical imaging and deep learning
Professor of Applied Mathematics
- Deep learning now outperforms traditional model-driven imaging methods by training on large datasets and achieving superior accuracy in tasks such as denoising and reconstruction.
- Its success depends on the training distribution; when data are limited or differ from what the network has seen, the model can hallucinate details or misinterpret images.
- Mathematical analysis provides essential guarantees, helping to explain, verify and stabilize neural networks and detect or predict their failures.
- A hybrid approach that combines neural networks with equation-based models seeks to merge data-driven accuracy with the universality and robustness of classical mathematics, benefiting fields where training data are scarce.
The emergence of deep learning
Mathematical image processing has been hit tremendously by the emergence and success of deep learning, and this is really when machine learning has become an extremely powerful tool, all of a sudden, for image processing. Before, we had more low-level machine learning in image processing, but it was not really something that was overshadowing everything else. The work that mathematical imaging people had done before used model-driven approaches based on mathematical equations, deriving these equations from first principles of understanding what the image is all about — what the problem with this image is, for instance, for denoising or deconvolution — and then thinking about how to turn it into a mathematical model that is well posed, that gives you a solution that is robust, that is generalizable and so on.
 © Shutterstock
© Shutterstock
Mathematics as a sanity check
In the work that I do, the philosophical implications of deep learning and the things I think we should worry about, or sometimes not worry about, are always triggered by the fact that we often use imaging as a tool to look at what we otherwise cannot look at. In medical imaging, we often look at people because we do not want to cut them open. In scientific imaging, we look at things that are often so tiny that we cannot see them with the naked eye. In these settings, it is really important that we can trust in the result of the image reconstruction algorithm — image denoising, image deconvolution, image inpainting algorithm.
 © Shutterstock
© Shutterstock
Having mathematics as a sanity check for what guarantees I can give for a super powerful deep learning approach that works wonderfully most of the time, but sometimes has this strange hallucination, helps me ask: how can I change this? Either the hallucination does not happen, which usually decreases accuracy and performance, maybe not ideal, or maybe I can live with the hallucinations if I can predict, detect and actually characterize them. I think mathematics is very important here not to forget.
Training deep learning
The key insight here is maybe to think a little bit about, in addition to the really impressive results that neural networks can achieve, what the limitations are. I always like to think about this by putting the two side by side. Deep learning can give you really accurate, very impressive results in detection and images, segmentation, image denoising and so on, but usually what you train it with is what you get as a result. If you train it only on images of cats, it will also only work on images of cats.
 © Shutterstock
© Shutterstock
If you apply it to an image that shows a dog, you might, if it is a denoising process, in addition to denoising, also turn your dog slightly into a cat-ish dog. These are the things that happen. It will depend on what you train it with, which is strongly contrasted to the traditional principled mathematical-equation type of approaches that are universal. They do not need to be trained. They work in every kind of setting. If you apply them to a medical image, they work the same way as they do on an astronomy image or an image of an art piece. They also work in the same way on cats and dogs. They are not as accurate as these deep learning approaches, but this is the natural bias-variance trade-off — the accuracy versus robustness, accuracy versus generalizability or universality, trade-off that you have.
A black box
 © Shutterstock
© Shutterstock
Deep neural networks are mostly a black box. Still, having also worked myself on mathematical foundations of neural networks for many years now, we are very far from what we can explain mathematically, which is for more simplistic neural network approaches than what is used in, for example, ChatGPT. Explainability with mathematical equations gives us a lot of trustworthiness, and we know that with neural networks things can also go wrong. The problem is we do not know when they go wrong because we cannot explain it.
The best of both worlds
The exciting thing is to bring them together. This is where the field of mathematical imaging as a whole is moving more and more, putting together the best of both worlds — getting the accuracy from neural networks, and the tremendous capability that neural networks have to characterize information content in imaging data, together with the principled way of mathematical equations-driven approaches, explainability and so on. Looking at this from the point of view of medical and scientific imaging, we may not have so much training data available, as in scientific imaging, where we often use imaging as a tool to explore things we have never seen before.
 © Shutterstock
© Shutterstock
We cannot afford to train on cats and then only see cats in these images, because we do not know whether there are cats or not, if that makes sense. I think this is where this hybrid methodology between partial differential equations, to take them as an example of more mathematical equation-driven approaches, and deep-learning approaches is really exciting. This is where the main excitement lies now for me and for many of my colleagues in the field.
Comparing reconstruction methods
A key insight in mathematical imaging, and why mathematical imaging people are thinking about these different methodologies to, for instance, reconstruct a computer tomography image from measurements that the machine has taken, is that there are various different reconstructions, infinitely many reconstructions, that fit the measurements in the same way. The art is to pick out the one that is most appropriate for what you want to do later, that is maybe most accurate in highlighting what is hidden in this image.

© Carola Schönlieb, DAMTP
How you do this, how these different methodologies improve upon enhancing the content in the image more and more accurately, is by complementing the data with prior information you have about what you are imaging. The data is limited — it is imperfect — which is also why different reconstructions match the data in the same way. You complement this with additional information you have about other types of CT scans that you have done in the past. This is an abdominal scan that you are looking at, where you have looked at lots of abdominal scans from other people before. You could use this information to say that humans are always a bit similar, so you can use this to enhance a specific image by averaging it, taking a mean with images that you had before — a more sophisticated mean, but you can think of it as a mean.
Data-driven processes
Before deep learning came in, we tried to model this prior information in terms of mathematical equations. What are the characteristic features in these abdominal scans? What is really important?
The most famous prior assumption that people had been using in medical imaging before deep learning was total variation regularization, which basically says the most important information in an image is where organs meet other organs, where there are boundaries between different objects, edges in an image. This is what we really want to preserve, and this is very important if we want to quantify things, like segment tumors in images later, but it is simplistic. This is where deep learning makes this prior information more data-driven based on a lot of abdominal scans you have looked at in the past, makes it so powerful and makes it more precise. One of these images, the first one, is the ground truth, a perfect computer tomography scan with perfect measurements. The other three are scans with lower radiation, radiating the patient less, which means you get data that is not as good.

© Carola Schönlieb, DAMTP
If you look at the last one, which is the data-driven one, it is the closest to the ground truth because, even with the worst measurements, by drawing connection to lots of other abdominal scans, it gets high accuracy and a lot of fine details out of the images.
Where deep learning falters
There are scenarios and settings where pure deep learning approaches can go wrong, in particular if we are in settings where we rely too much on this highly accurate prior information, settings where the data is very limited and where we have much less data than we would need to reconstruct an image from it confidently. One technique that comes to mind, used in the biomedical domain, is limited angle tomography, where you have a whole viewpoint of the object you are looking at that you have not measured. In settings where you have huge gaps, like in the inpainting example, when we think about image inpainting for images (restoration of images), if we think of this in the transform in the medical domain, if we have large gaps in the data, this is where deep learning can go wrong — if it takes too much of the prior information into account and does not respect the information content in the data. It might make up things that are not there. If you look at this example that we have in the bottom left image and compare that with the ground truth, you see that it has totally made up things like bones that should not be there. The whole shape of the body is different, so this is where you see cats where there are no cats.
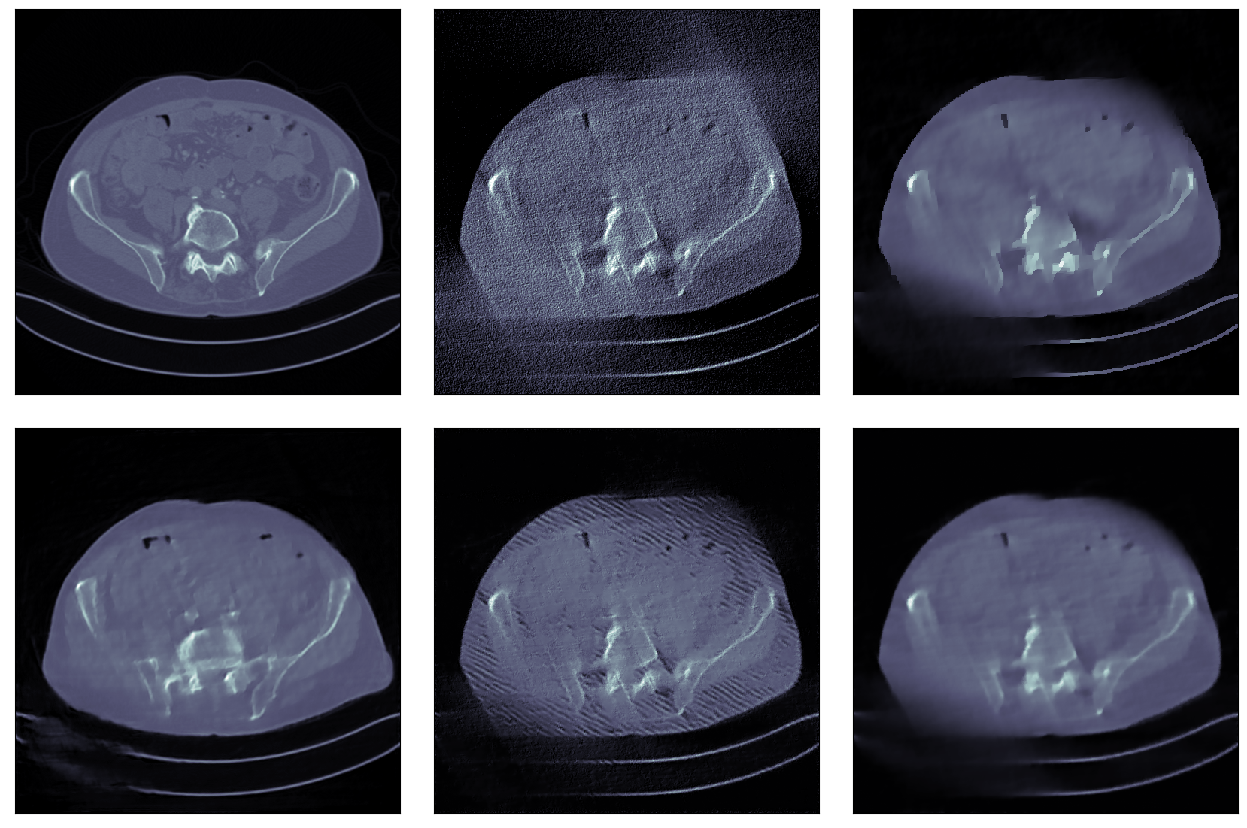
© Carola Schönlieb, DAMTP
Mathematical challenges in deep learning
If you try to pin down or formalize what deep learning is, it is basically optimizing — minimizing a loss function, a mathematical function that is fed with training data, under the constraint that what you are optimizing are parameters in a neural network that has a certain architecture. It is already a mathematical problem. It is a constrained optimization problem where the constraint is that you are optimizing parameters in a neural network with a certain architecture and so on. It lends itself to mathematical analysis. The problem is that it is super complex, very high dimensional, and the deepness of neural networks — where you have nested layers in which one operation is nested within another one within another one — is what makes it such a complex mathematical problem.

© Shutterstock
There are many mathematically formalizable questions out there that have direct practical relevance. The question of generalizability — how can we quantify how generalizable a method is or how can we quantify what type of data, what type of functions, this neural network can approximate — is an approximation theory question. What can I do to my neural network to make it more robust? We hear a lot about adversarial robustness and adversarial instabilities of deep learning classifiers. All of a sudden, when you change an image invisibly, it gives you a totally different classification. It contains a lot of interesting mathematical problems, and it is also our duty to help and contribute to unveiling the mysteries of this black box.
Complementary approaches
In the context of imaging in particular, I think the main way forward and the main area where mathematical imaging people are at the moment influencing the field is structure-preserving deep learning: imposing constraints on neural networks that might come in terms of equations or symmetries of the solutions that you expect, constraints that help you impose certain properties of the solution that you know the solution should have, or that help you to impose adversarial stability, making the deep learning process more robust.

© Shutterstock
That is one direction, and the other is to use deep learning as a plug-and-play tool in the more robust mathematical equation approaches that we have, to enhance these and embed deep learning into a framework that we understand, that is explainable and that we know is robust.
Editor’s note: This article has been faithfully transcribed from the original interview filmed with the author, and carefully edited and proofread. Edit date: 2025
Discover more about
imaging and deep learning
Arridge, S., Maass, P., Öktem, O., Schönlieb, C.B. Solving inverse problems using data-driven models. Acta Numerica 28, 1-174, 2019
Lunz, S., Öktem, O., Schönlieb, C.B. Adversarial Regularizers in Inverse Problems. Advances in neural information processing systems 31, 2018
Kiss, M.B., Biguri, A., Shumaylov, Z., Sherry, F., Joost Batenburg, K., Schönlieb, C.B., Lucka, F. Benchmarking learned algorithms for computed tomography image reconstruction tasks. Applied Mathematics for Modern Challenges, 2025, 3: 1-43.
Celledoni, E., Ehrhardt, M.J., Etmann, C., McLachlan, R.I., Owren, B., Schönlieb, C.B., Sherry, F. Structure-preserving deep learning. European journal of applied mathematics 32 (5), 888-936, 2021
De los Reyes, J.C., Schönlieb, C.B. Image denoising: learning the noise model via nonsmooth PDE-constrained optimization.. Inverse Problems & Imaging 7 (4), 2013
Mukherjee, S., Hauptmann, A., Öktem, O., Pereyra, M., Schönlieb, C.B. Learned reconstruction methods with convergence guarantees: A survey of concepts and applications. IEEE Signal Processing Magazine 40 (1), 164-182, 2023