One really exciting component of the application‑side work that I do is the collaboration with art historians and conservators on art restoration, and also analysis and interpretation of art, where we are looking at digitized versions of whatever art piece we are examining. When I look at a piece of art, it is definitely not like in the movie "A Beautiful Mind", where I only see numbers. What I see actually entices the curiosity of what I cannot see or what has been lost.
Mathematics in art
Professor of Applied Mathematics
- Mathematical imaging frames art restoration as an inverse problem, using data such as spectral or X-ray scans to infer what lies beneath the visible surface.
- In a 16th-century children’s primer, infrared scans showed the original Adam and Eve before the addition of skirts, and partial differential equations inpainted colors to digitally recreate the scene.
- Different mathematical models, ranging from partial differential equations to neural networks, produce varied yet plausible restorations, so choosing the right assumptions becomes a creative decision.
- The notorious Ecce Homo fresco shows how neglecting solid modelling and evidence can yield implausible outcomes, underscoring the need to balance prior beliefs with data.
Enticing curiosity
 © Shutterstock
© Shutterstock
Looking at the invisible
A lot of times, if I look at a particular historical piece, the artwork has gone through a process. It may have survived centuries, various political events and several weather‑related incidents, so it has endured a lot, and you can see this in the painting. There may also be manipulations that have happened to this art piece where people have overpainted something or removed elements. Where we come in as mathematical imaging specialists is we try to go back and discover what has been lost — or maybe not completely lost, but what is no longer visible to the human eye.
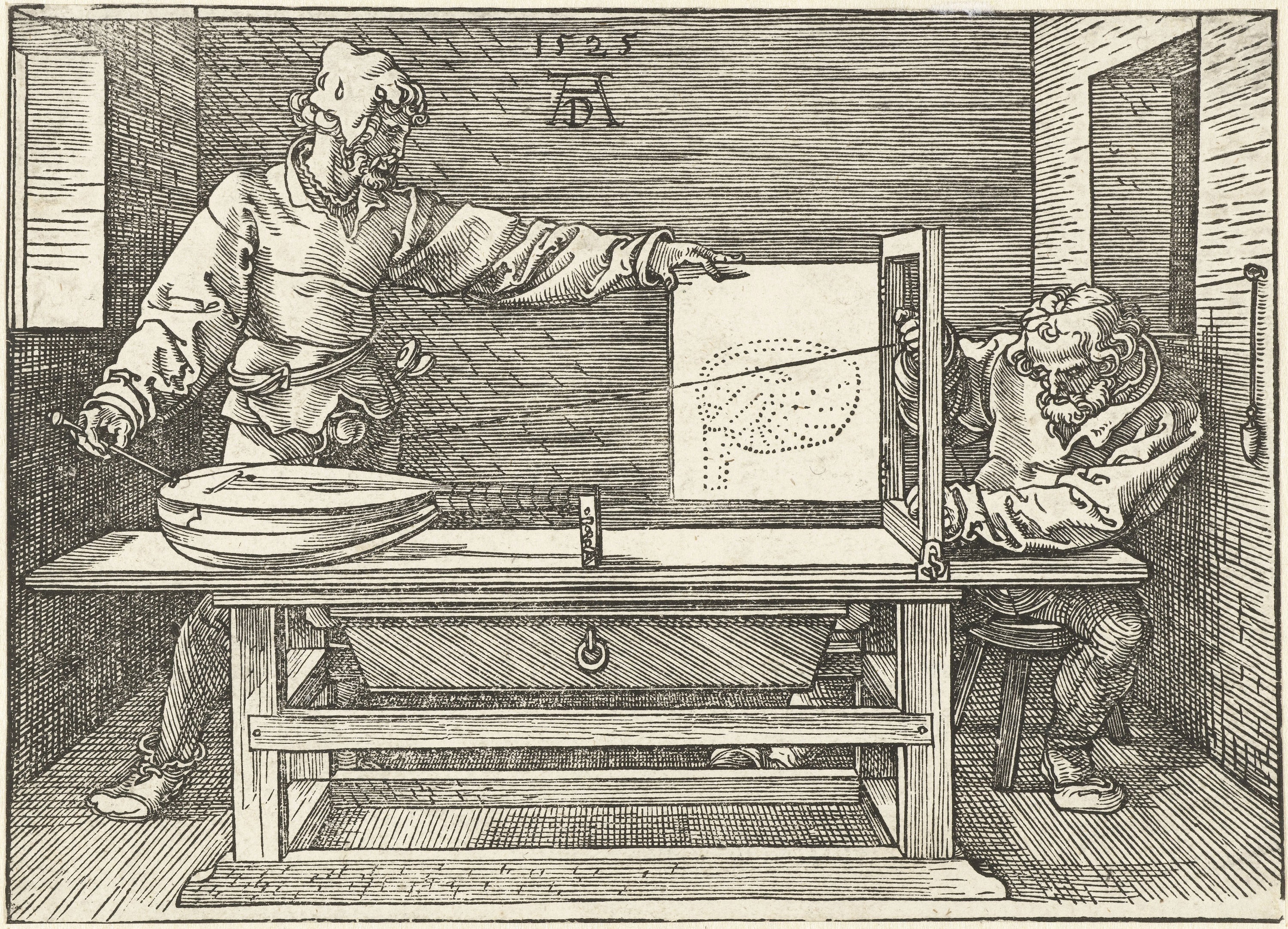 Man drawing a lute © Albrecht Dürer VIA Shutterstock
Man drawing a lute © Albrecht Dürer VIA Shutterstock
In mathematical terms, you can phrase this as an inverse problem. You take a measurement — a digital photograph, in our case — of an image. In scientific imaging, we do not just take a photograph; we might take a more sophisticated image, like multispectral imaging that captures wavelengths beyond the visible light spectrum, such as infrared imaging, or we can also perform X‑ray imaging on a painting. I look at this data and want to understand, based on it, what the original image, or the image at various moments in time, looked like before. This is an inverse problem. It is about having measurements but being interested in something that is hidden in them, and it is about inverting — hence “inverse” — the forward process, which is the history that has happened to this art piece.
An illuminated manuscript
This illuminated manuscript from the 16th century is a children’s primer commissioned by the Queen of Brittany for her daughter, Claude. On the one hand, it teaches the alphabet, but at the same time it tells the story of biblical creation.

The Primer of Claude of France © Fitzwilliam Museum
In the illuminations that accompany the text, you see Adam and Eve in Paradise, how they live there, how Eve eats the apple and how they are expelled. When the manuscript was created, Adam and Eve were painted as naked; as you know from the biblical story, in Paradise they are without sin. Later on, the book came into the possession of a different owner who was not happy with a children’s book featuring naked figures, so another artist was commissioned to overpaint Adam and Eve with skirts.
Finding the structure underneath
What we did was see whether we could digitally show how these illuminations looked before this overpainting happened. Illuminations are very specific because they are so fragile that they would never be physically restored — they could break if you do too much to them. In addition to standard photographs of the illuminations, the museum captured spectral images, particularly infrared images. The infrared data allowed us to look through the skirts and detect the structure underneath.
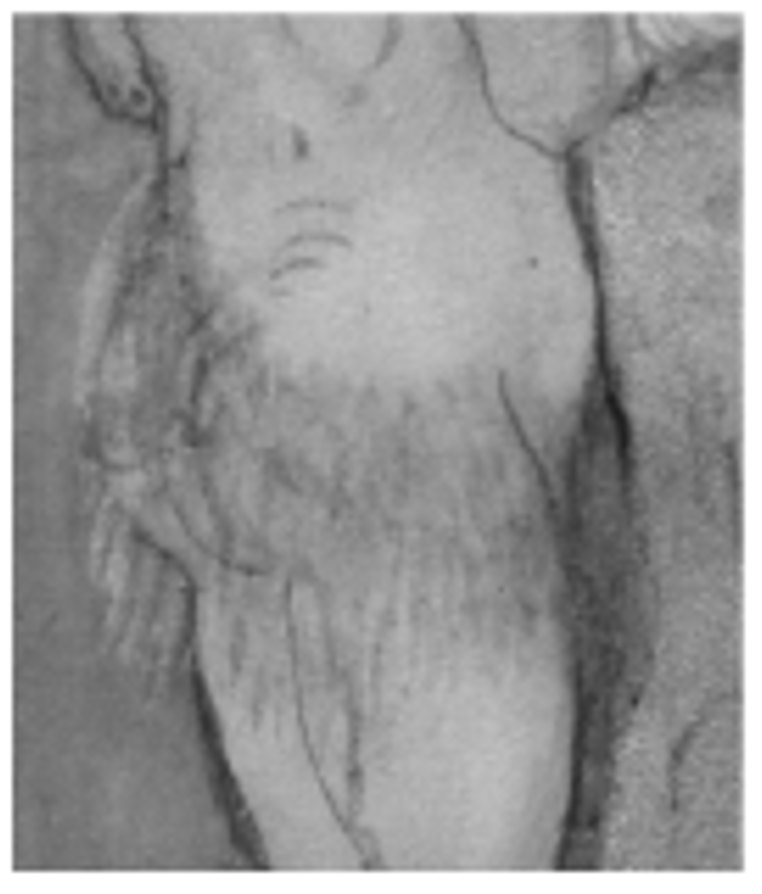 © Fitzwilliam Museum
© Fitzwilliam Museum
We then combined the color photograph — with its colors, textures and so on — with the structural outline of Eve and Adam's bodies from the infrared image, and inpainted the colors into the area of the skirts following the structures provided by the infrared data.
 © Fitzwilliam Museum
© Fitzwilliam Museum
Equations versus deep learning
We used a particular partial differential equation. At the time, deep learning was not quite such a big thing. The digital restoration you see was therefore produced with a partial differential equation that could give at least an idea of how it might have looked before. This was interesting, because it allowed us to showcase the result prior to an exhibition at the Fitzwilliam Museum about color and illuminations, where they displayed the physical manuscript alongside our digital restoration. It was a great opportunity to show the impact that looking back in time can have — you can visually imagine the original much better when you see it — and a great way to communicate how powerful mathematics is.
Mathematics as an art
The inpainting result (the digital restoration result) will depend on the partial differential equation I use. If I use another equation, it will look slightly different. If I use something other than a partial differential equation, such as a neural network, it will look different again. Depending on the image‑processing methodology, I get different results. All of them may be plausible, but they depend heavily on the assumptions you put into the restoration process.
 © Shutterstock
© Shutterstock
Thinking about this, the question arises: is mathematics applied to art also an art in itself, an art of finding the right methodology for the restoration? I would say yes. Mathematics is a formalized language with grammar that tells you what you can and cannot do, but within those constraints you have the freedom to put ideas together in whatever way you want. To some extent, mathematics applied anywhere, not just in art, is an art in itself, in finding the right models.
Choosing the right models
Another thing you can see when developing the partial differential equation — apart from the mathematician being an artist — is that it is crucial to discuss the right equations with the art historians and conservators. They can tell you the art‑historical context you might need to consider when modelling your equation or even when performing the scientific imaging, without them suspecting that these parts had been overpainted. No one might have looked at this before. They can also explain how they physically do restoration.
 Section of a medieval fresco © Carola Schönlieb, MACH, courtesy of Wolfgang Baatz
Section of a medieval fresco © Carola Schönlieb, MACH, courtesy of Wolfgang Baatz
One of the first partial differential equations developed by Marcelo Bertalmio and colleagues was modeled after talking to museum artists; they look at the hole (the damaged part in the picture), observe structures that arrive there, such as color edges, and propagate them inward. This is almost a recipe for writing down a transport‑type equation, which Marcelo and colleagues did.
The beautiful thing about art and mathematics is that they are mutually inspiring. The art historians particularly appreciate using mathematical equations like partial differential equations because they provide an objective way to handle inpainting, which is very ambiguous. You can never go back in time and prove that what you have done is correct; you can only make an educated guess. These equations help you do that, and you can explain how they work in a formalized way that the art historians can understand and debate.
Ecce Homo
The main driver for developing methodologies, differential equations, to do the image inpainting is to create something visually plausible.
The inpainting result depends on the modeling assumptions that you put into the differential equation or whatever mathematical model you use to solve the inpainting. A funny example I like to show is that these modeling assumptions, or any prior conceptions you might have, influence how you restore images.
A Spanish woman near Zaragoza, a frequent visitor to a church, saw a heavily damaged portrait of Jesus Christ. The portrait had been in the church for more than 100 years and was damaged, though you could still make out the main characteristics. She felt so awful about this that she took up the task of restoring the portrait herself — and she did.
 Ecce Homo © Elías García Martínez, Diocese of Tarazona via Wikimedia and Cecilia Giménez (restoration attempt)
Ecce Homo © Elías García Martínez, Diocese of Tarazona via Wikimedia and Cecilia Giménez (restoration attempt)
Her restored version went through the news a lot a couple of years ago. The original portrait is titled Ecce Homo; the new version she created was jokingly called Ecce Mono. It looks like a monkey rather than Jesus Christ. Of course, what you think is good or not is somewhat subjective, but most of us will agree that it is no longer close to the portrait we started with.
This illustrates that in image restoration and inpainting, or inverse problems in imaging in general, everything depends on the prior information you put in and how closely you stick to the data, to the evidence — in this case, the damaged Jesus Christ painting or fresco.
Editor’s note: This article has been faithfully transcribed from the original interview filmed with the author, and carefully edited and proofread. Edit date: 2025
Discover more about
uncovering the invisible
Schönlieb, C. B. (2015). Partial differential equation methods for image inpainting. Cambridge University Press.
Parisotto, S., Vitoria, P., Ballester, C.,Bugeau, A. Reynolds, S., Schönlieb, C. (2025). The Art of Inpainting: Mathematical Methods for the Virtual Restoration of Illuminated Manuscripts. Cambridge University Press.
Calatroni, L., d’Autume, M., Hocking, R., Panayotova, S., Parisotto, S., Ricciardi, P., & Schönlieb, C. B. (2018). Unveiling the invisible: Mathematical methods for restoring and interpreting illuminated manuscripts. Heritage Science, 6, Article 56.
Hocking, L. R., MacKenzie, R., & Schönlieb, C. B. (2017). GuideFill: GPU-accelerated, artist-guided geometric inpainting for 3D conversion of film. SIAM Journal on Imaging Sciences, 10(4), 2049–2090.
Sober, B., Bucklow, S., Daly, N., Daubechies, I., Dragotti, P.L.. Higgitt, C., Huang, J.J., Pižurica, A., Pu, W., Reynolds, S., Rodrigues, M., Schönlieb, C.B., Yan, S. (2022)Revealing and reconstructing hidden or lost features in art investigation. IEEE BITS the Information Theory Magazine 2 (1), 4-19, 2022
Bertalmío, M., Sapiro, G., Caselles, V., Ballester, C. (2000). Image inpainting. 27th Annual Conference on Computer Graphics and Interactive Techniques.