Fluid mechanics is a wonderful branch of applied mathematics. Wonderful, because there are applications on all length scales: from the micro scale at the level of the human cell to the macro scale of galaxies in the cosmos. Fluids, in this context, refer to liquids, gases or fully ionised gases, sometimes called plasmas. The miracle is that on all these length scales, provided the fluid is regarded as a continuum, the dynamics is governed by a single equation known as the Navier–Stokes equation. This equation was discovered by Navier, a French engineer in the 19th century, and again a bit later – and by an entirely different method – by George Gabriel Stokes, who was Lucasian Professor of Mathematics at Cambridge.
Fluid mechanics and the problem of turbulence
Emeritus Professor of Mathematical Physics
- In fluid mechanics, there are applications on all length scales: from the micro scale at the level of the human cell to the macro scale of galaxies in the cosmos. Fluids, in this context, refer to liquids, gases or fully ionised gases.
- If you increase the length scale or decrease the viscosity, you get to a point where the flows are no longer steady. This leads to the phenomenon of turbulence.
- Turbulence is still an unsolved problem, despite the huge efforts of mathematicians, computational scientists and experimentalists over the last century.
Fluid mechanics
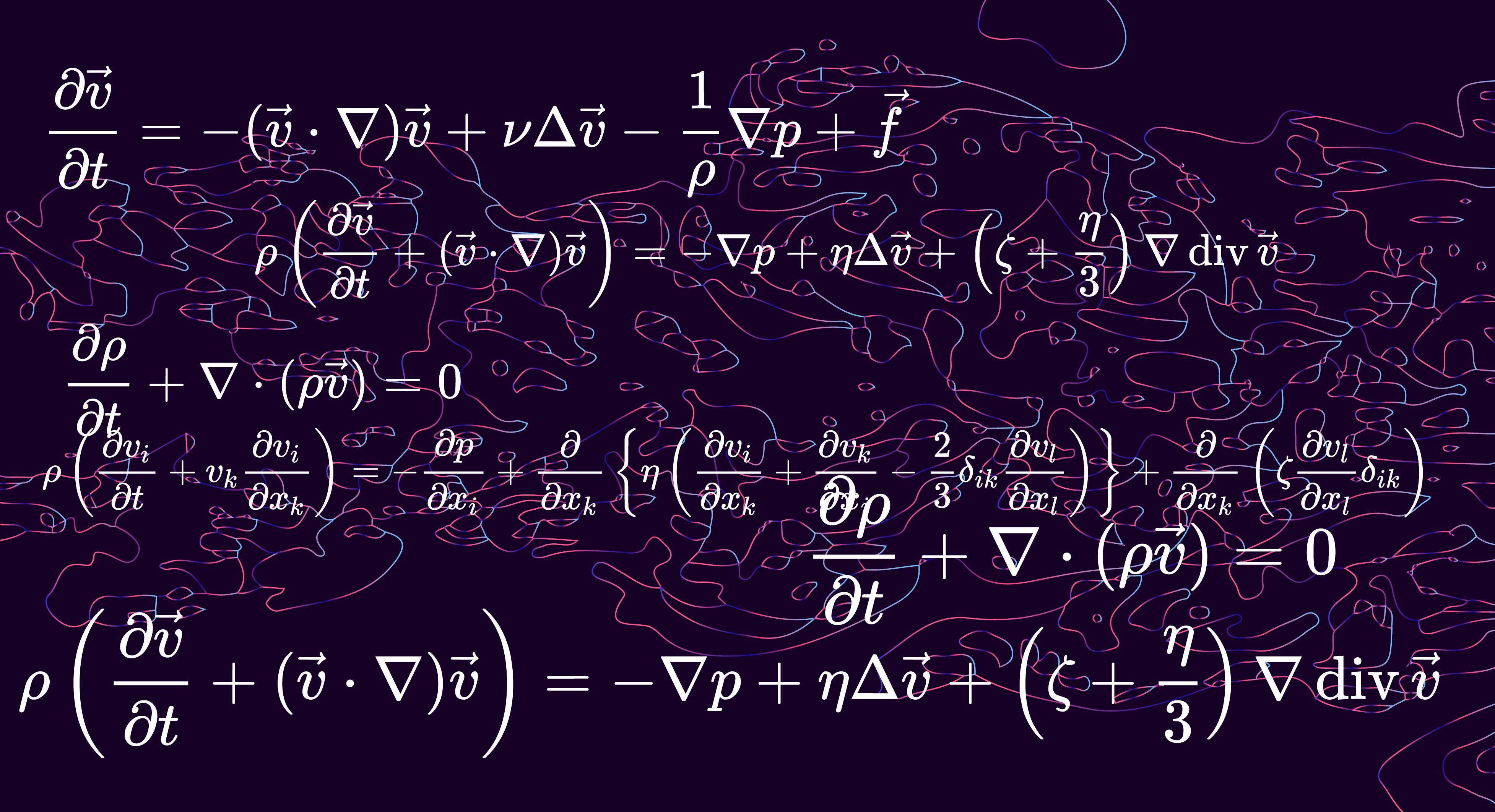
Photo by local_doctor
The turbulence phenomenon
If one considers the very small scale, or fluids that are very viscous (which implies they have strong internal friction), then the flows tend to be smooth and steady. For example, if you put a spoonful of fluid like treacle on a plate, you’ll observe that it spreads quite slowly and steadily. The radius increases as a function of time and, believe it or not, that functional dependence goes like time to the power one eighth. It’s quite a difficult result to prove, but it’s rather typical of the results that can be obtained by mathematical methods in fluid mechanics.
However, if you increase the length scale or decrease the viscosity, you get to a point where the flows are no longer steady. They become highly unstable, and this leads to the phenomenon of turbulence. Turbulence characterises flows, for example, in the atmosphere or in the oceans, which are obviously on a large-length scale and have fairly low viscosity. In these scenarios, it is important that viscosity is still there, or non-zero. It’s especially important for the science of flight, for example: airplanes couldn’t fly if the air wasn’t endowed with a little bit of internal friction.
The problem of turbulence
The problem of turbulence, and the reason why it’s such an intriguing and challenging problem, is that there is what we describe as a “cascade of energy” from large scales, which could be of the order of hundreds of kilometres in the atmosphere down to very small scales of millimetres in the atmosphere. The small scale is the scale at which viscosity intervenes and dissipates the energy of the turbulence, and it’s the understanding of that cascade process that is so challenging and makes the problem of turbulence. It’s still an unsolved problem, despite the huge efforts of mathematicians, computational scientists and experimentalists over the last century.
Why is it so difficult to solve?

Photo by Igor Stepovik
In 1961, I listened to a lecture from the famous Theodore von Kármán, who said that when he died and met his creator, he would ask him two questions. One would be about quantum electrodynamics; the other would be about the problem of turbulence. He said that he expected to get an answer on the first question, but not, alas, on the second.
Why is this so difficult, from a mathematical point of view? It’s described by the Navier–Stokes equation, which is a non-linear partial differential equation involving at least four variables: three components of velocity, and the pressure at every point in the fluid. There may be other variables involved, as well.
It’s non-linear, which is always a challenge for mathematicians, and it’s also non-local in that the pressure field has very long-distance effects. It’s also dissipative, because of the influence of viscosity. The combination of these three effects makes this one of the most difficult problems arising in describing natural phenomena.
Two ways of approaching the problem
This particular problem can be approached in two different ways. The first way is to try to prove that no matter what initial condition you start with, the solution cannot develop a singularity within a finite time, meaning it cannot diverge towards the infinite within a specified time frame.
There is a very highly developed method in the domain that’s known as functional analysis, which mathematicians use to try to solve the problem in this way. The alternative approach is to try to prove that there is a singularity at finite time by choosing a suitably contrived initial condition. That’s the approach that I’ve been trying to follow, without success, over the last few years. Neither of these approaches has as yet led to an answer to the problem. If you were to conduct a Gallup Poll today, mathematicians and physicists across the world would still be pretty evenly divided as to whether the answer to this question is yes or no.
The stages of trying to solve a problem
There is a curiosity involved. You run into a problem – you perhaps hear about it at a conference, or during a lecture – and you think to yourself, oh, perhaps I can solve that one. It doesn’t look too difficult. You start to scribble notes about it. You struggle over it for days, then weeks and then months, and you realise that, really, it is very difficult. The longer you struggle with it, the more challenging it becomes, and the more desperate you become to find a solution one way or another.
Just occasionally, you have a breakthrough. You make a discovery. You solve a problem and you have a great sense of achievement. There’s a greater excitement in solving a problem that nobody else has succeeded in solving before. I’ve had that experience only twice in my lifetime. But that’s enough. Once would have been enough. It’s a wonderful, exciting sensation. It’s like, in a way, a treasure hunt. You’re looking for a needle in a haystack. If you find it, it’s so exciting.
The discovery of an invariant

Photo by German Vizulis
One such discovery, in 1969, was of a new invariant – something that is constant in time – of the Euler equations. Euler produced the equations for ideal fluids, or zero-viscosity fluids, in 1756. So, it’s an equation that has a very long history. I discovered this invariant in 1969 and, some years later, as so often happens, I found out that it had been discovered eight years previously by a French mathematician, Jean-Louis Moreau.
But my achievement was to realise that this invariant had a topological character. This established a bridge between fluid mechanics and topology that I’ve been trying to develop ever since. So, there was a great excitement about that discovery for me, in 1969, and a realisation that it would be an opening for what turned out to be huge new developments in the subject.
Discover more about
turbulent flows
Moffatt, H. K. (2012). Homogeneous turbulence: an introductory review. Journal of Turbulence, 13(1), N39.
Moffatt, H. K., Kida, S., & Ohkitani, K. (1994). Stretched vortices: the sinews of turbulence; high Reynolds number asymptotics. J. Fluid Mech, 259, 241–264.
Moffatt, H. K. (1981). Some developments in the theory of turbulence. J. Fluid Mech, 106, 27–47.